Today's study
1.모집단 & 표본
2. 분포(Distribution): 정규분포
3.표본평균의 분포
4.가설검정: 귀무가설, 대립가설, 유의수준, 유의확률
5. 일표본 검정
집단
- 모집단(population): 일반적으로 "인구"
- 나라(state)에서 인구수를 세는 이유: 세금, 군대
- 따라서, 일반적인 모집단이 인구가 됨
- 분석하고자 하는 대상을 모집단으로 두면 됨
- 그러나 모집단 전체를 분석하기엔 비용, 시간이 매우 큼
e.g. 한국정부에서 인구주택 총조사에 드는 비용 3000억/년 * 5년
- 따라서, 표본을 선택 - 표본(sample)
- 표본의 대표성 확보 중요
: 해당 표본이 모집단을 대변할 수 있는지
- 대표성이 확보되었다 여겨도 모집단과 동일x 유사하다고 표현해야 - 데이터(data)
- 분석(탐색적 데이터 분석): EDA
- figure, graph, 평균... data의 특징, 패턴을 분석함
- 통계분석(가설검정)
: a, b의 값이 차이가 우연에 의한 것인지 or 필연에 의한 것인지를 따지는 것
(유의미한 차이 or 무의미한 차이) - 인공지능
- ML 머신러닝
- DL 딥러닝
- LLM 거대언어모델(ML, DL 포함): 정확성을 중요하게 둠(예측, 분류 등)
--> 인공지능의 결과를 domain을 해결할 때(협업처) 근거를 설명해 줄 수 있어야함
--> 이것이 통계/분석 - 추론(inference)
- 표본의 분석결과로 모집단을 예측하는 것
- 일부의 결과에서 전체를 판단하는 것
- 종류
1) 추정(estimation)
- 모집단의 평균값(mu)을 모르기때문에 대략 표본의 평균(x bar)으로 예측하는 것
- 종류: 점추정, point estimation (e.g. 연봉 예측, 1.5억) / 구간추정, interval estimation (e.g. 1.5+alpha)
2) 가상검증 - 분석순서
population --> sample --> data --> analysis
- 모 표준편차(sigma): 모집단의 평균과 data의 값이 다른지 측정한 값
- 분포의 종류
- 균등분포(균일 분포)

- 정규분포(normal distribution)
- 모집단(표본x)의 data 값이 평균(모 평균, mu) 값의 좌우 대칭인 값
- Histogram은 표본의 data로 그리는 것

- 특징
1) 모집단의 data값이 평균값 대칭
2) +- 1 sigma: 0.6826

3) +- 2sigma: 0.9544

4) += 3sigma : 0.9974
5) 나머지: 0.0026 --> data가 이 분포에 있을 때 놀랄일! ㅎ(=유의미한 값)
- 특정 값에 대한 히스토그램 상 면적값을 구하라 할 때, 해당 "분포"를 모르면 구할 수 없음
--> 특정 값에 대한 값을 구할 때, 해당 값의 분포가 무엇인지를 먼저 알아야.

- 모집단이정규분포이면 표본집단도 정규분포

- 표준화(standarditation)
- 예측하기 위해 사용
- 데이터의 단위를 표준 편차로 나누어서 새로운 척도로 변환하는 과정
- 표준화를 위해서
1) 모양을 통일시켜줘야함
2) 단위 간의 비교
- 구하는 식
모집단에서의 x 표준화 - 가설검정
- 가설(hypothesis): 모집단(모수: parameter)에 대한 입장
- 가설의 종류
1) 귀무가설(Null hypothesis, Ho): 모집단에 대한 기존의 입장
2) 대립가설(Alternative hypothesis, H1 or HA): 모집단에 대한 새로운 입장 - e.g. 귀무/대립 가설 중 선택할 것은? (유의확률 정의)
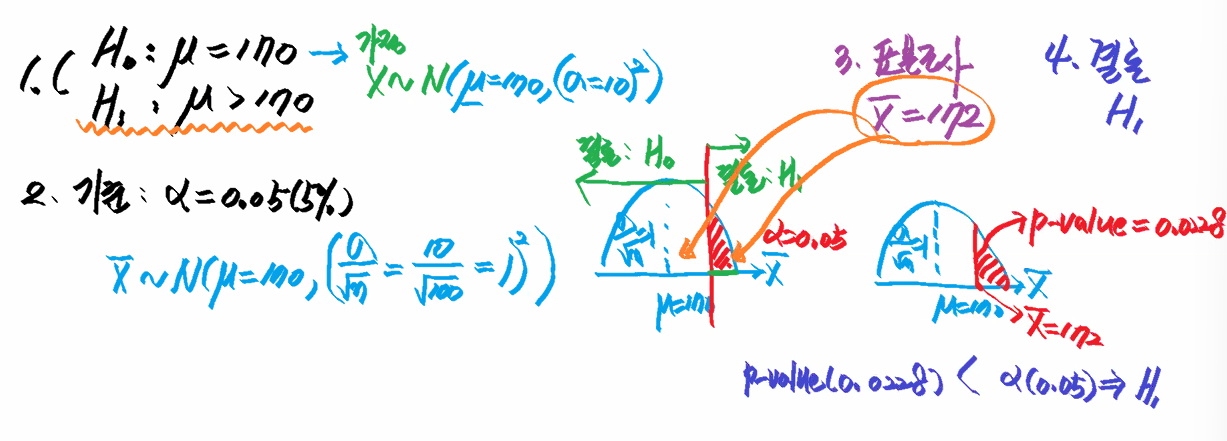
- Ho: mu(모평균) =170cm
- H1: mu > 170cm
- 이때, 표본평균(x bar)가 약 170cm 이면 귀무가설이 유력
- 어디까지가 크다고 할 수 있을까? --> 기준필요
- 가정(Assumption): 이 모집단은 정규분포라고 가정
- 어느 값부터 대립가설이 귀무와 다르다고 정할까?
--> 사람들이 정하기를 alpha error가 0.05(5%) 이상일 때 다르다고 정함
- 유의확률(p-value)
- 표본에서 관찰한 값(표본 평균)이 귀무가설이 맞다는 가정에서의 분포에서 얼마나 일어날까를 알려주는 값
- 유의확률이 작다는 것 = 표본에서 관찰한 값이 귀무가설이 맞다는 가정하에서 일어나기 어려운데 일어난 상황
- 0.05% 이하일때 유의미하다 --> 대립가설로 간다 - 유의수준(alpha) = 0.05% 기준
- 유의수준 0.05% 이하이면 유의하다
<p-value Summary>
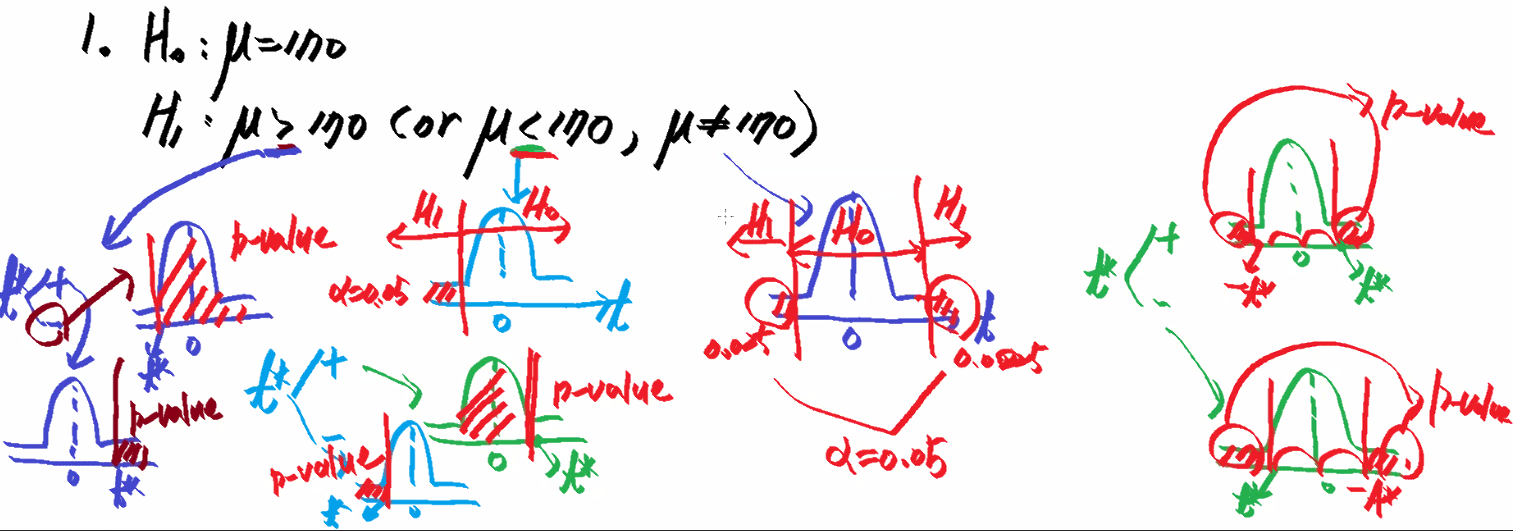
- p-value 설정
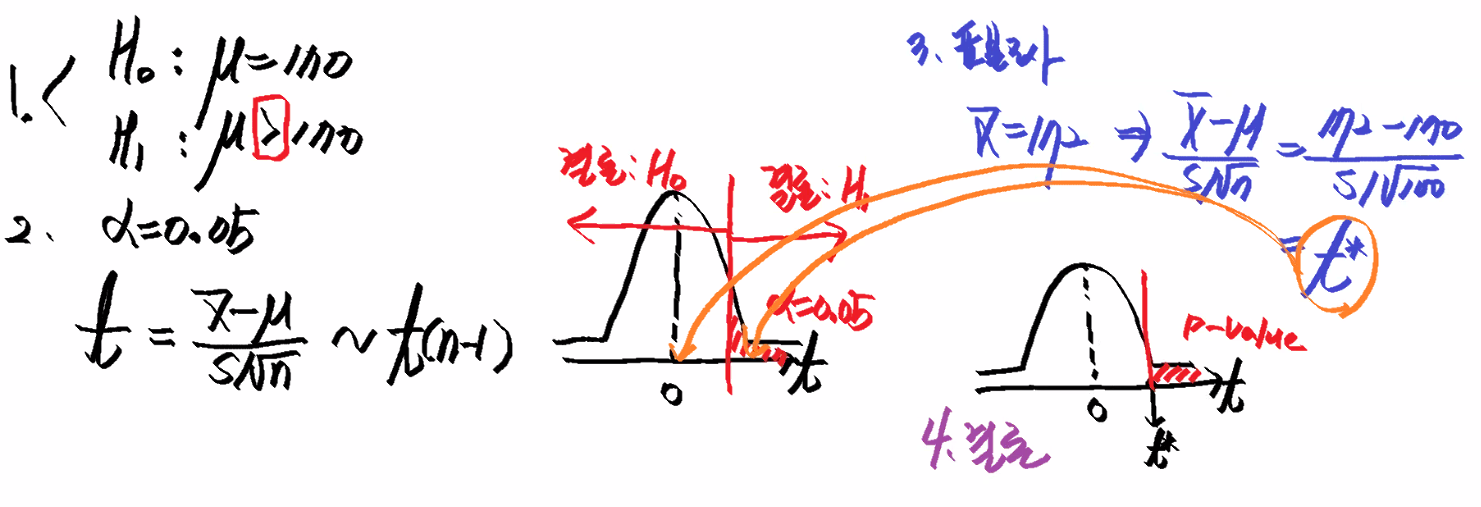
- 일표본 t 검정(one sample t-test)
<Summary>
- One sample test
- 모집단의 평균이 기존보다 커졌는지/ 작아졌는지/ 달라졌는지 분석하는 방법
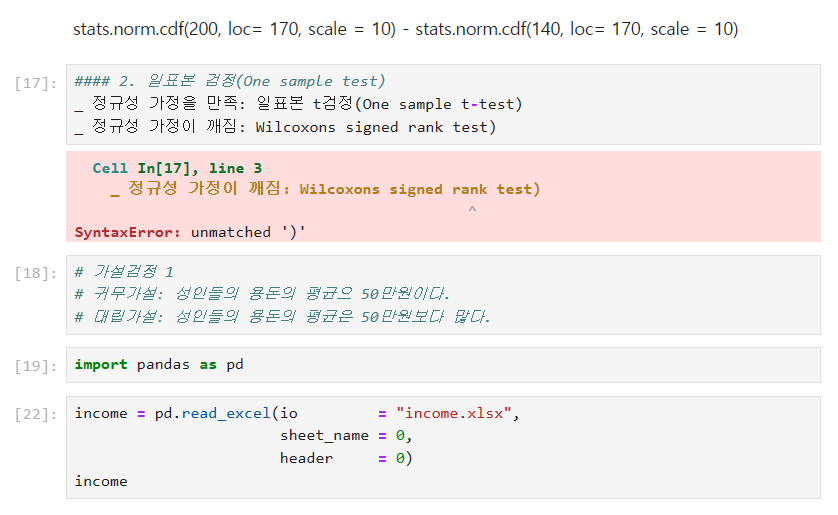
일표본 검정
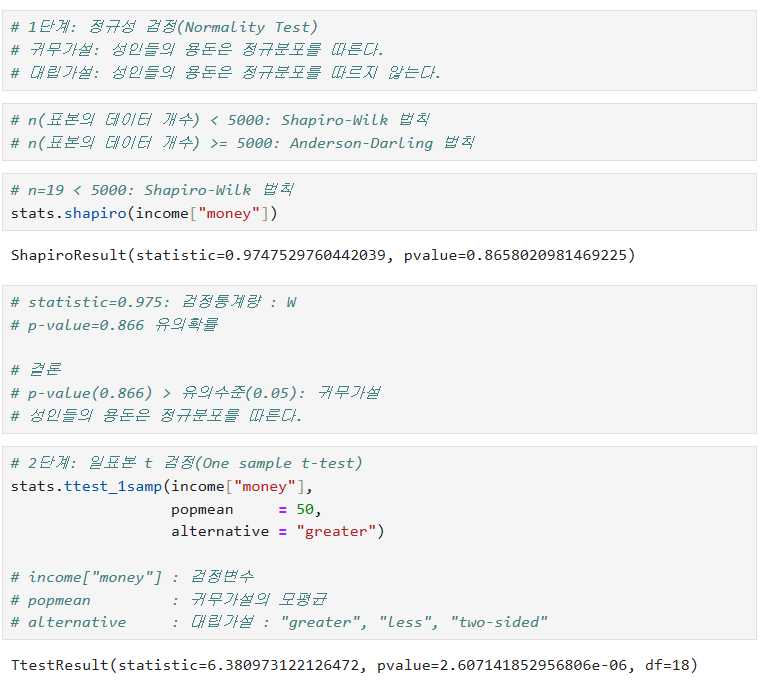
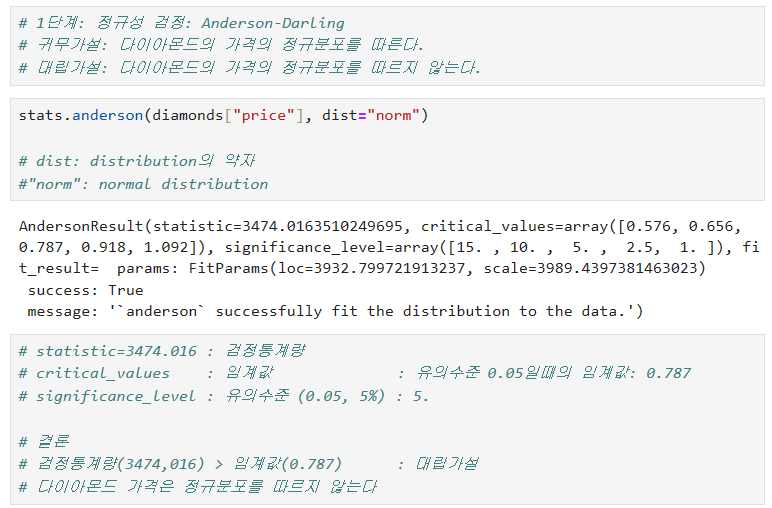
1) 정규성 가정을 만족(정규 분포일 경우): 일표본 t 검정 (one sample t-test)
- 모수적 방법(parametic method)
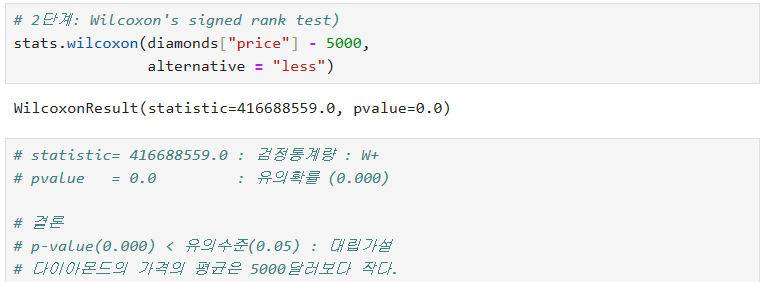
2) 정규성 가정이 깨짐(비정규 분포일 경우): Wilcoxon's signed rank test
- 비 모수적 방법(non parametic method)
p.s.
Tool: 문제 + 통계(데이터), 컴퓨터, 수학
--> 문제를 정의할 수 있는 능력: problem definition (AI시대에 중요한 능력)
--> 좋은 질문을 할 수 있는 능력 - - 내가 개발하고 싶은 domain이 무엇인지 확실히 인지하고 tool을 다루기
- Tool + domain 지식 = AI 기술
- 문제(domain): 의료, 심리, 농업, 체육, 금융, 제조 ...
Python으로 구해보기
- 패키지(Package) 로딩(Loading) 하기
- Loading: 패키지를 메모리(RAM)에 올리는 기능
- stats package 설치 후 import scipy.stats as stats
- stats.norm.cdf(x값 , loc=평균값, 표준편차)
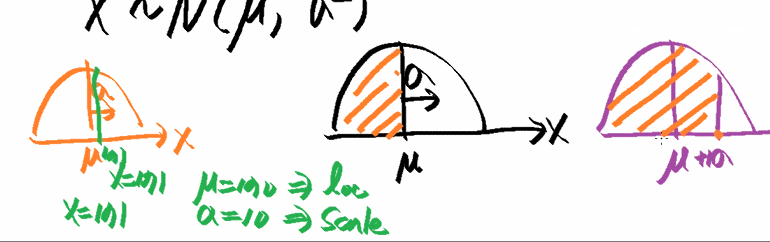
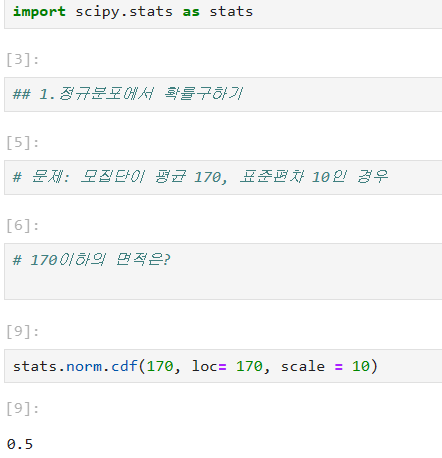
- 정규분포

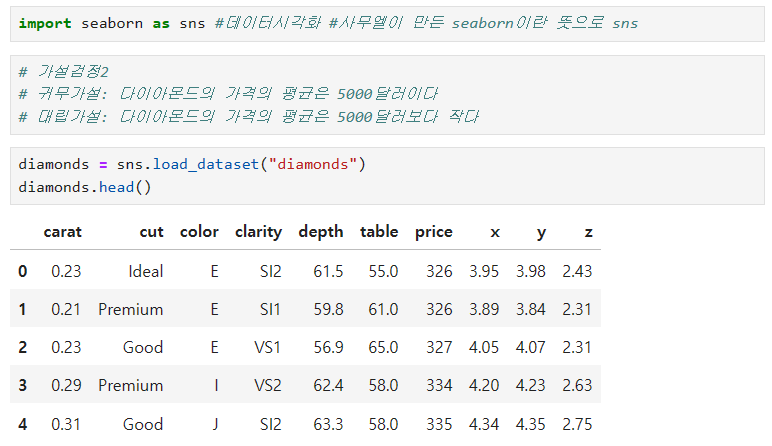
- 비정규 분포
** Flow chart를 꼭 작성하라.
시간이 걸려도 바로 coding하지말고 flow chart를 짠 뒤에 coding하기